Regulación estatal de los Monopolios naturales (página 2)

1. Una de las soluciones más antiguas al problema
   del monopolio natural es la fijación de
   un precio
   igual al costo marginal por parte del Estado.
   Debido a que con esta política de tarificación se
   logra el máximo excedente del mercado,
   esta asignación de los recursos
   es llamada primer orden ("first best"). Su
   aplicación hoy en día es bastante limitada
   porque supone la necesidad de una subvención estatal
   para cubrir el déficit en el que la
   compañía incurre. Como se puede apreciar en
   el grafico siguiente esta situación implica un costo
   medio mayor al ingreso marginal lo que repercute en un
   beneficio negativo para la firma. Debe tenerse en cuenta
   que la necesidad de cubrir el déficit con ingresos
   fiscales puede ocasionar distorsión en los precios
   de otros sectores económicos lo que podría
   acarrear mayores ineficiencias que la propia
   solución.

2. Fijación del costo
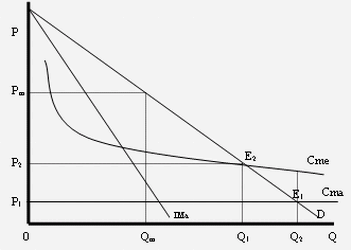
   marginal y el precio

   Por otra parte, existe otra solución sobre
   la base de la tarificación administrada por el
   Estado. Esta consiste en que los consumidores paguen
   los costos
   totales de producción fijando un precio igual al
   costo medio. Se trata de un óptimo de segundo orden
   ("second best"). Su principal ventaja es liberar al Estado
   de la correspondiente subvención aun cuando existan
   ciertas ineficiencias: una disminución del output
   genera un mayor precio comparativamente con el modelo
   anterior y por ende una pérdida de excedente del
   consumidor que es apropiado por el
   monopolista.

   

   E1: Óptimo de primer
   orden

   E2: Óptimo de segundo
   orden

   Ambos modelos
   no cuentan con mecanismos que estimulen a las empresas
   monopólicas a realizar inversiones destinadas a la mejora de la
   eficiencia económica. Bajo los
   supuestos de información perfecta y un sesgo
   tarifario nulo, cualquier inversión que resulte en una baja de
   las curvas de costo marginal o medio ocasionará que
   el precio también se reduzca. Como los costos y el
   precio se mueven en paralelo y en la misma cuantía,
   el beneficio no se modificará.

   Otra manera de obtener un óptimo de segundo
   orden sin recurrir a una regulación directa por
   parte del Estado es la competencia por el mercado propuesta
   por Demsetz en 1968. Se trata de que los potenciales
   entrantes compitan por el derecho de abastecer un mercado.
   Siempre que exista un número suficiente de empresas
   interesadas, la competencia (mediante ofertas) para obtener
   o mantener la franquicia llevaran a que el precio se
   aproxime al costo medio unitario.

   Este modelo es ampliamente utilizada en la
   Republica Argentina en especial en los corredores viales.
   El modelo de Demsetz es atrayente debido a que sugiere que
   la competencia puede ser posible inclusive cuando existen
   economías de escala.
   Otra de las características positivas de este modelo
   es la liberación del Estado de las tareas usuales de
   regulación.

   Una segunda manera de lograr un óptimo de
   segundo orden es mediante las formulaciones del concepto de
   "contestabilidad del mercado." La idea es que la
   empresa incumbente no podrá elevar el precio por
   arriba del costo medio unitario debido a que existen otras
   firmas que al percatarse de los beneficios extraordinarios
   querrán entrar al mercado. Para que esto sea
   posible, aparte de un número apreciable de empresas,
   no debe existir ninguna barrera legal a la entrada ni
   costos hundidos.

3. Fijación del costo medio y el
   precio

   Consiste en incorporar a los costos de
   producción del bien o servicio
   una cantidad estipulada como beneficio normal unitario que
   debiera tener la empresa,
   similar a la técnica del "mark up" seguida por los
   gerentes de las firmás. Se trata de limitar en forma
   indirecta los beneficios del monopolista restringiendo la
   rentabilidad del capital
   invertido fijando una tasa "justa", que se conoce como
   "tasa base." Este tipo de regulación tolera que el
   precio supere el costo marginal.

   Si la empresa realiza su labor eficientemente y
   produce al costo mínimo, la tasa de rendimiento que
   obtendría sería la tasa competitiva de la
   inversión realizada. Pero esta circunstancia
   raramente se cumple en la práctica como se demuestra
   más adelante mediante el "efecto
   Averch-Jonsons".

   Existen muchos factores que dificultan la labor
   del organismo gubernamental encargado de determinar la tasa
   de rendimiento competitiva del capital para un periodo
   dado. En principio, existe una falla de información
   asimétrica en donde el regulador no obtiene
   información suficiente sobre las variables que maneja la empresa, ocasionando
   errores de medición en la "tasa base."
   Circunstancias como las épocas de inflación
   durante las cuales resulta bastante difícil evaluar
   los costos del capital invertido (a un costo de
   reposición que cambia continuamente o un costo
   historio subvaluado) hacen, entre otras causas, muy
   compleja su correcta fijación.

   Ante el dilema de fijar una tasa de rendimiento
   del capital inferior o superior a la tasa competitiva se
   plantea en el primer caso la propia supervivencia de la
   empresa o el deterioro de la calidad
   del servicio, mientras que en el segundo caso daría
   lugar a unos beneficios extraordinarios de carácter cuasi-monopólico
   situación que el regulador pretende evitar. Averch y
   Jonson (1962) opinan que los reguladores se inclinan sobre
   esta última opción. Plantearon la respuesta
   mediante un análisis de las consecuencias de una
   fijación de la tasa de rendimiento superior al coste
   del capital, calculada como un porcentaje sobre el capital
   empleado a un nivel que debería ser el
   eficiente.

   Este comportamiento puede ilustrase
   analítica y gráficamente con el siguiente
   sencillo modelo:

   Sea la función de producción:
   q=f(K,L) K=Capital , L= Trabajo

   C= rK+wL r y w precios de los factores

   Si definimos la tasa de rendimiento del capital
   como la razón entre el exceso de los ingresos
   totales sobre los costes laborales respecto al volumen
   total de capital:

   t = It – W L ó
   p f(K,L) – W L Siendo p el precio del
   producto

   K K

   Cuando el regulador permite una tasa de
   rendimiento "t", el objetivo
   de maximización del beneficio de la empresa sujeto a
   la restricción WL + tK – p f(K,L)=0, (t>r) se
   resuelve con el Lagrangiano siguiente,

   S= p f(K,L) – wL – rK –
   l [wL + tK – p
   f(K,L)]

   ¶ S
   = p ¶ f – w –
   l [w – p ¶ f ] = 0

   ¶ L ¶ L ¶
   L

   ¶ S
   = p ¶ f – r –
   l [t – p ¶ f ] = 0

   ¶ K ¶ K ¶
   K

   ¶ S
   = wL + tK – pf (K,L)
   = 0

   ¶ l

   La primera de estas condiciones se cumple cuando,
   p ¶ f/¶ L= w es decir, el valor de
   la productividad marginal del factor trabajo
   es igual a su precio.

   La segunda condición se desarrolla como
   sigue:

   p ¶ f
   – r + l t – l p ¶
   f = 0

   ¶ K ¶ K

   (1- l ) p ¶ f = r – l
   t

   ¶ K

   p ¶ f
   = r + l t – l r +
   l r = r + l
   (t-r)

   ¶ K 1 +
   l 1 + l

    

   – Sí l =0, p
   ¶ f = r , el resultado es similar al
   obtenido con el factor trabajo.

   ¶ K

   En este caso la regulación no
   tendría efecto alguno y el monopolista se
   comportaría normalmente como maximizador de
   beneficios.

   – Si l =1, el
   lagrangiano quedaría reducido a S=(t-r)K,
   situación que en el caso de autorizar un valor
   t>r significaría que la empresa podría
   expandir el capital invertido en cantidades ilimitadas.
   Este es un supuesto ilógico y por lo tanto se
   rechazará.

   Por lo antes mencionado el valor de l deberá estar comprendido en entre
   0 y 1.

   -Si 0<l <1, la
   segunda condición nos muestra
   que p ¶ f < r ,
   es decir,

   ¶ K

   la fijación de una tasa de rendimiento del
   capital "t" por el regulador origina el empleo
   de una cantidad mayor de capital con una productividad
   física menor que si no hubiera sido
   regulada, hay por lo tanto una sobrecapitalización
   de la empresa.

   

   -Qo curva isocuanta de un determinado
   nivel de producción

   -Eo (Ko,Lo)
   socialmente óptimo

   -E1 (K1,L1) con
   regulación

   Si no hubiera regulación, el costo de
   producir Qo estaría representado por la
   isocosto AB, en cambio,
   la sobrecapitalización de la empresa regulada lleva
   a que la nueva curva isocosto sea A´B´ que
   supone un mayor gasto y por lo tanto una ineficiencia en el
   empleo del input de capital.

   Se ha establecido que la regulación de
   una
   empresa por medio de la tasa de rendimiento lleva a que
   esta se sobrecapitalice en orden de obtener así
   mayores beneficios. Tampoco hay que dejar de lado los
   efectos negativos que provoca el sobre-empleo del factor
   capital en la eficiencia de la empresa y en el empleo del
   factor trabajo.

   

   ¿Pero hasta que punto es tolerable esta
   ineficiencia? Una respuesta estaría en la
   posibilidad de que se incremente el nivel de
   producción que mantenía el monopolista no
   regulado. Con esto se compensarían ganancias
   sociales y costos de la regulación como se muestra
   en la siguiente figura.

   El monopolista sin regulación estatal
   establecería un nivel de producción Qm y un
   precio Pm mediante la regla Cma=Ima produciendo una perdida
   de eficiencia irrecuperable representada por el triangulo
   ABC. En cambio, el monopolio regulado, con un costo
   superior debido a la regulación (g) y un incremento
   en la producción hasta Qr produce en el mercado una
   perdida de eficiencia representada por el triangulo
   DEC.

   La comparación de los excedentes en ambos
   equilibrios ofrecería una ganancia social (ABED) con
   un incremento en los costos antes inexistentes (FEHG) y la
   pérdida irrecuperable por ineficiencia del monopolio
   queda reducida al triángulo DEC. El resultado de la
   regulación dependerá de la magnitud de las
   áreas afectadas con la condición de una
   ampliación del nivel de
   producción.

   La gran ventaja de este modelo se concreta en una
   cierta y relativa facilidad para conocer la tasa
   competitiva de rendimiento del capital, así como los
   beneficios y el capital invertido por la
   empresa.

4. Regulación de la tasa de
   rendimiento
5. PRI-X (Retail price index-X)

Uno de los problemas
centrales que plantea la regulación de los monopolios
según Yarrow (1994), es la de diseñar un sistema que cree
incentivos
adecuados para que la empresa regulada fomente la
reducción de sus costos, innovación y mejora de la eficiencia
interna.

En numerosos países, las empresas, en especial
las de servicios
públicos que han sido privatizadas, estuvieron
acompañadas de controles regulatorios que en vez de
limitar la tasa de rendimientos hacen hincapié en la
fijación de los incrementos de precios.

El modelo RPI-X limita los incrementos medios de
precios en un determinado año teniendo en cuenta la tasa
de inflación (RPI) de una canasta de bienes menos
las mejoras estimadas por el regulador sobre el grado de
crecimiento de la productividad (eficiencia X) de la
firma.

Se trata de un método de
regulación de "precio tope" que fue utilizado por primera
vez en Gran Bretaña, concretamente en la British
Telecommunication Company y propuesto por Littlechild en 1983.
Posteriormente se aplicaría a las empresas de gas, agua y
servicios
considerados como esenciales.

El termino RPI representa el porcentaje de
inflación como medida de precios al por menor de los
principales insumos de la industria. Se
trata generalmente de un índice de Laspeyres, que compara
los gastos del
año base con los de un período determinado para una
cesta de bienes de consumo
inalterada.

RPI= å Pi
Xio

å
Pio Xio

"X" es la tasa a la que caen los precios regulados con
relación al índice de precios agregado. Registra
las mejoras en la eficiencia y el crecimiento de la demanda que
repercute favorablemente gracias a las economías de
escala. Los valores de
la variable "X" dependen de cada industria y son de
difícil calculo pero esta se puede interpretar como una
estimación de los incrementos en productividad de la
empresa como propone Vogelsand (1989):

Xi = å
Pit-1
(Zit–Zit-1)
, donde "Xi" es una suma de incrementos de outputs
menos inputs

å
Pit-1
Zit-1

La idea básica del modelo es que la empresa no
puede aumentar sus precios en una cuantía que exceda a la
diferencia entre el índice de precios y el factor de
eficiencia. Los precios regulados deben caer en promedio al menos
un "X" por ciento al año. Esta caída
dependerá del valor estimado de dicho factor. A modo de
ejemplo podemos ilustrar su cálculo
como sigue: sea el precio del bien en el año base de 100
pesos, la inflación 10% y el porcentaje de eficiencia
estimado del 5%; el precio
P1=Po+RPI-X=100+(100*10%)-(100*5%)=
100+10-5= $105.

Dos cuestiones relacionadas al modelo deben tenerse en
cuenta cuidadosamente: la calidad del producto
ofertado y el periodo de vigencia de la
regulación.

Existe la posibilidad de que la empresa empeore la
calidad del servicio para así obtener mayores beneficios
cuando la regulación ha sido fijada exclusivamente en
términos de precio. Esto constituye un riesgo que la
autoridad
reguladora no puede obviar, en especial para aquellos bienes que
son de carácter público como el agua,
energía y saneamiento, entre otros. Es por lo dicho
anteriormente que se debe tener en cuenta el cumplimiento de un
estándar de calidad minino y exigible.

La otra cuestión de carácter
crítico es el plazo de vigencia de los valores
estimados por la regla RPI-X. El regulador se encuentra inmerso
en un conflicto de
interés
por las partes interesadas en el servicio (empresa-cliente), las
cuales actuaran para modificar los precios a su favor. El
tiempo de
actualización no será lo mismo para empresas que
necesiten grandes o pequeñas inversiones. Tal es el caso
de las industrias del
agua y energía y otras en donde un plazo de cinco
años puede considerarse como un corto plazo y así
darse situaciones de desinversión.

El problema fundamental del modelo es la elección
o estimación adecuada del factor "X" y el periodo de
actualización del mismo. Este debe ser elegido de tal
forma que responda a la naturaleza de
la regulación: el mejoramiento del nivel general de
bienestar. No se debe caen en soluciones simplistas que
consideren una actualización de la regla en forma
excesiva, argumentando un exceso de poder por
parte del monopolio.

Según Ordóñez de Haro (2003), el
período de vigencia debe ser superior al año,
normalmente entre 3 y 5 años dependiendo de las
posibilidades de mejoras tecnológicas y ahorradoras de
costos de la industria. Ejemplo de esto es la ley chilena que
obliga a la Comisión Nacional de Energía a realizar
el cálculo cada cuatro años.

Al no controlarse directamente los beneficios, la
empresa regulada puede mantenerse dentro de los topes otorgados y
maximizar sus ganancias. Estos beneficios permanecerán
durante el periodo de vigencia de la regla. Finalizado
éste, el regulador tendrá la posibilidad de
modificar el valor de "X" reduciendo o aumentando la tasa de
ganancia futura de la empresa.

Como se mencionó anteriormente, debe tenerse sumo
cuidado al establecer el período de actualización
del factor "X" debido a que un reajuste periódico
puede reducir el estímulo de la empresa a obtener una
mayor eficiencia ya que a la larga esta será
contrarrestada por la futura actualización. Otra
deficiencia del modelo surge de la información
asimétrica que detenta el regulado, problemática
que puede ocasionar fallas de mayor o menor grado cuando la
empresa infla sus costos o el capital invertido en el
período base de cálculo de la regla con el fin de
lograr una fijación de precios beneficiosa para los
próximos años.

Conclusiones y recomendaciones

Debido a la importancia que los monopolios naturales
tienen en la vida de las personas como proveedores de
bienes esenciales tales como el agua, gas, electricidad y
saneamiento es imperativo la necesidad de una adecuada
regulación. En la Republica Argentina queda pendiente una
apropiada discusión respecto a que modelo regulatorio es
más factible para cada industria en orden de evitar los
problemas de desabastecimiento y empeoramiento de la calidad que
estamos sufriendo. A diferencia del presente trabajo se deben
tener en consideración otras variables como la
protección del medio ambiente, la
calidad del servicio brindado y el sesgo tarifario que sufren las
empresas en especial en las épocas de
inflación.

BIBLIOGRAFÍA

• Averch y Jonson (1962): "A behavior of the firm under
  regulatiory constraint", American Economic Review, Diciembre,
  pp. 1052-1069.
• Handbook of Industrial Organization (1992): vol. II.
  Editado por Richard Schmalensee. North Holland,
  Ámsterdam.
• Ley 26.156 (1999): Gobierno de la
  Republica Argentina.
• Mitnick, (1989): "La Economía
  Política de la Regulación". Fondo de Cultura
  Económica de México.
• OCDE (1996): "local telecommunication Competition:
  Developments and Policy Issues", Paris
• OCDE (1997): "Reformer la Reglementation
  environnementale dans les pays de l´OCDE", vol. I. Etudes
  sectorielles. Paris
• Ordóñez de Haro (2003): "La
  regulación económica: el problema del Monopolio
  Natural". Universidad
  de Málaga.
• Vogelsang (1989): "Price cap regulation of
  Telecommunication services: a long run approach" en
  Deregulation of utilities. Boston.
• Yarrow (1994): "The Economics of regulation", Londres
  y Nueva York, pp. 35-46.

Autor:

Julian Daniel Egea

UNIVERSIDAD NACIONAL DE ROSARIO

FACULTAD DE CIENCIAS
ECONÓMICAS

Cátedra: MICROECONOMÍA I

ROSARIO 2004